Documentation for CSV and Excel Files
Description of the CSV File Type
Files with a comma separated value (*.csv) extension are in plain text. They contain characters stored in a flat, nonproprietary format and can be opened by most computer programs. Each *.csv file contains a set of tabular data, with each record delineated by a line break and each field within a record delineated by a comma. A field that contains commas as part of its content has the additional delineation of a quote mark character before and after the field's contents. When a quote mark character is part of a field's content, it is included as two consecutive ""quote mark"" characters.
Computers with Microsoft Excel installed open *.csv files in Excel by default, with the fields automatically arranged appropriately in columns. Other database programs also open *.csv files with the fields appropriately arranged.
The 780 CSV files (i.e., "NSDUHsubstatePValueTab#-#_2016.csv") reflect the 780 Excel tables,1 and they contain the table title, table notes, column headings, and data. The webpage at https://www.samhsa.gov/data/ for the 2014-2016 NSDUH state p value tables includes a hyperlinked table of contents on the first sheet of the Excel file that combines all of the Excel tables, as well as a ZIP file containing all of the individual CSV files. Additionally, the ZIP file includes a text file with a list of the table numbers and titles.
How to Use the P Value Tables
The p values contained in these tables for each outcome and age group can be used to test the null hypothesis of no difference between population percentages for the following types of comparisons:
- total United States versus census region (within the table, to find the p value, go to the census region row, then to the Total United States column),
- total United States versus state (within the table, to find the p value, go to the state row, then to the Total United States column),
- total United States versus substate region (within the table, to find the p value, go to the substate region row, then to the Total United States column),
- census region versus census region (within the table, to find the p value, go to the second census region's row, then navigate to the column of the other census region),
- census region versus state (within the table, to find the p value, go to the state row, then navigate to the census region column),
- census region versus substate region (within the table, to find the p value, go to the substate region row, then navigate to the census region column),
- state versus state (within the table, to find the p value, go to the second state's row, then navigate to the column of the other state),
- state versus substate region (within the table, to find the p value, go to the second state's row or the substate region's row, then navigate to the column of the other area), and
- substate region versus substate region (within the table, to find the p value, go to the second substate region's row, then navigate to the column of the other substate region).
For example, within any given table, by scrolling across Alabama's state row to the South's census region column, the p value found will determine whether Alabama's state population percentage and the South's census region population percentage are significantly different for a particular outcome of interest. By scrolling across the row for Alabama's Region 2 to the column for the state of Alabama, the p value found will determine whether Alabama's state population percentage and Alabama's Region 2 population percentage are significantly different for a particular outcome of interest (in any Alabama table). Similarly, by scrolling across the row for Colorado's Region 7 to the column for Region 1 of Colorado, the p value found will determine whether Region 7's population percentage and Region 1's population percentage are significantly different for a particular outcome of interest (in any Colorado table). Note that the tests included here are for a given outcome and age group.2
The following example describes how to test the null hypothesis of no difference between population percentages in the national file. Table 6 in the national file contains p values for past month alcohol use among individuals aged 12 or older for all of the substate regions in the United States and for each state and census region. To find the p value for testing the null hypothesis of no difference between population percentages for past month alcohol use between two large metropolitan areas, such as Region 11 (Los Angeles) in California and Region 2: New York City in New York, scroll to the row for Region 2: New York City and navigate to the column for Region 11 (Los Angeles). That p value is 0.004. Thus, the hypothesis of no difference—that is, the Region 11 (Los Angeles), California, population percentage for past month alcohol use is the same as the Region 2: New York City, New York, population percentage for past month alcohol use—is rejected at the 5 percent level of significance, meaning that the two prevalence rates are statistically different. Note that the small area estimates for Region 11 (Los Angeles), California, and Region 2: New York City, New York, are 46.96 and 50.74 percent, respectively.3 Using the same procedure, if users want to test differences in past month alcohol use small area estimates between two adjacent substate regions that are in two different states (e.g., the Badlands region in North Dakota and Region 1 in South Dakota), they can use the national file to find the p value (i.e., 0.834).
The following example describes how to test the null hypothesis of no difference between population percentages in a state file. Table 2.2 in Alaska's file contains p values for past month marijuana use among individuals aged 12 or older for the four substate regions in Alaska and for the West census region. The p value for testing the null hypothesis of no difference between Anchorage, Alaska, and the West census region population percentages for past month marijuana use is 0.002, which is found by scrolling to the row for Anchorage and navigating to the column for the West census region. Thus, the hypothesis of no difference (i.e., the Anchorage population percentage for past month marijuana use is the same as the West census region population percentage for past month marijuana use) is rejected at the 5 percent level of significance, meaning that the two prevalence rates are statistically different. Note that the Anchorage, Alaska, and the West census region estimates are 13.51 and 10.48 percent, respectively.4
Comparison between Two Small Area Population Percentages
To produce substate region, state, census region, and national small area estimates, the 2014-2016 NSDUH data were modeled using the method discussed in Section B.1 of the "2014-2016 NSDUH: Guide to Substate Tables and Summary of Small Area Estimation Methodology" document at https://www.samhsa.gov/data/. This modeling results in 1,250 Markov Chain Monte Carlo (MCMC) samples that are used here to calculate p values for testing the null hypothesis of no difference between two small area population percentages.
Let 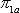 and
and 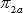 denote the 2014-2016 population percentages of two areas (e.g., state 1 vs. state 2 or state 1 vs. national, or substate region 1 vs. substate region 2) for age group-a. The difference between
denote the 2014-2016 population percentages of two areas (e.g., state 1 vs. state 2 or state 1 vs. national, or substate region 1 vs. substate region 2) for age group-a. The difference between 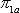 and
and 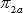 is defined in terms of the log-odds ratio,
is defined in terms of the log-odds ratio, 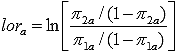 , where ln denotes the natural logarithm, as opposed to the simple difference (
, where ln denotes the natural logarithm, as opposed to the simple difference (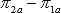 ) because the posterior distribution of the log-odds ratio is closer to Gaussian than the posterior distribution of the simple difference.
) because the posterior distribution of the log-odds ratio is closer to Gaussian than the posterior distribution of the simple difference.
An estimate, 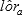 , of
, of 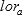 is given by the average of the 1,250 MCMC sample-based log odds ratios. Let
is given by the average of the 1,250 MCMC sample-based log odds ratios. Let 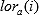 denote the log-odds ratio for the i-th MCMC sample. That is,
denote the log-odds ratio for the i-th MCMC sample. That is,
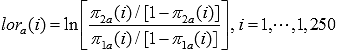 .
.
Then 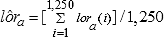 , and the variance of
, and the variance of 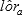 is given by
is given by 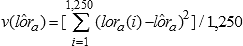 .
.
To calculate the p value for testing the null hypothesis of no difference, (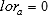 ), it is assumed that the posterior distribution of
), it is assumed that the posterior distribution of 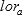 is normal with
is normal with 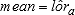 and
and 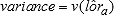 . With (
. With (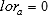 ), the Bayes p value or significance level for the null hypothesis of no difference is
), the Bayes p value or significance level for the null hypothesis of no difference is 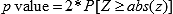 , where
, where 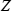 is a standard normal random variate,
is a standard normal random variate, 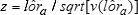 , and
, and 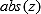 denotes the absolute value of
denotes the absolute value of  . This Bayesian significance level (or p value) for the null value of
. This Bayesian significance level (or p value) for the null value of 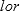 , say
, say 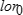 , is defined following Rubin5 as the posterior probability for the collection of the
, is defined following Rubin5 as the posterior probability for the collection of the 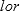 values that are less likely or have smaller posterior density
values that are less likely or have smaller posterior density 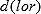 than the null (no change) value
than the null (no change) value 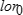 . That is,
. That is, 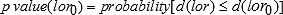 . With the posterior distribution of
. With the posterior distribution of 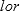 approximately normal,
approximately normal, 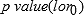 is given by the above expression. If the p value is less than 0.05, then it can be stated that the estimates for the two areas are statistically different from each other.
is given by the above expression. If the p value is less than 0.05, then it can be stated that the estimates for the two areas are statistically different from each other.
